In a previous article I presented how to compute the skew angle of a digitized text document by using the Probabilistic Hough Transform. In the last article I presented how to compute a bounding box using OpenCV, this method was also used to compute the skew angle but with a reduced accuracy compared to the first method.

Test Set

We will be using the same small test set as before:

The naming convention for those images is simple, the first letter stands for the sign of the angle (p for plus, m for minus) and the following number is the value of the angle.
m8.jpg has therefore been rotated by an angle of -8 degrees.

Bounding Box

In this article I will assume we have computed the skew angle of each image with a good accuracy and we now want to rotate the text by this angle value. We therefore declare a function called deskew that takes as parameters the path to the image to process and the skew angle.

void deskew(const char* filename, double angle)
{
  cv::Mat img = cv::imread(filename, 0);
 
  cv::bitwise_not(img, img);
 
  std::vector<cv::Point> points;
  cv::Mat_<uchar>::iterator it = img.begin<uchar>();
  cv::Mat_<uchar>::iterator end = img.end<uchar>();
  for (; it != end; ++it)
    if (*it)
      points.push_back(it.pos());
 
  cv::RotatedRect box = cv::minAreaRect(cv::Mat(points));

This code is similar to the previous article: we load the image, invert black and white and compute the minimum bounding box. However this time there is no preprocessing stage because we want the bounding box of the whole text.

Rotation

We compute the rotation matrix using the corresponding OpenCV function, we specify the center of the rotation (the center of our bounding box), the rotation angle (the skew angle) and the scale factor (none here).

  cv::Mat rot_mat = cv::getRotationMatrix2D(box.center, angle, 1);

Now that we have the rotation matrix, we can apply the geometric transformation using the function warpAffine:

  cv::Mat rotated;
  cv::warpAffine(img, rotated, rot_mat, img.size(), cv::INTER_CUBIC);

The 4th argument is the interpolation method. Interpolation is important in this situation, when applying the transformation matrix, some pixels in the destination image might have no predecessor from the source image (think of scaling with a factor 2). Those pixels have no defined value, and the role of interpolation is to fill those gaps by computing a value using the local neighborhood of this pixel.
The quality of the output and the execution speed depends on the method chosen.

The simplest (and fastest) interpolation method is INTER_NEAREST, but it yields awful results:
.

There are four other interpolation methods: INTER_NEAREST, INTER_AREA, INTER_CUBIC and INTER_LANCSOZ4.
For our example those 4 methods yielded visually similar results.
The rotated image using INTER_CUBIC (bicubic interpolation):

Cropping

We should now crop the image in order to remove borders:

  cv::Size box_size = box.size;
  if (box.angle < -45.)
    std::swap(box_size.width, box_size.height);
  cv::Mat cropped;
  cv::getRectSubPix(rotated, box_size, box.center, cropped);

As mentioned in the previous article, if the skew angle is positive, the angle of the bounding box is below -45 degrees because the angle is given by taking as a reference a "vertical" rectangle, i.e. with the height greater than the width.
Therefore, if the angle is positive, we swap height and width before calling the cropping function.

Cropping is made using getRectSubPix, you must specify the input image, the size of the output image, the center of the rectangle and finally the output image.
We use the original center because the center of a rotation is invariant through this transformation.
This function works at a sub-pixel accuracy (hence its name): the center of the rectangle can be a floating point value.

The cropped image:

To better understand the problem we have with positive angles, here what you would get without the correction:

Display

This is a small demo so let's display the original image, the rotated image and the cropped image:

  cv::imshow("Original", img);
  cv::imshow("Rotated", rotated);
  cv::imshow("Cropped", cropped);
  cv::waitKey(0);
}

That's it ! It's really simple to rotate an image with OpenCV !

In a previous article I presented how to compute the skew angle of a digitized text document by using the Probabilistic Hough Transform.
In this article we will present another method in order to calculate this angle , this method is less acurate than the previous one but our goal is rather to introduce two new OpenCV techniques: image scan with an iterator and computing the minimum bounding box of a set of points.

Bounding Box

The minimum bounding box of a set of 2D points set is the smallest rectangle (i.e. with smallest area) that contains all the points of the set. Given an image representing a text, like this one:

The points of our 2D set are all the white pixels forming the different letters.
If we can compute the bounding box of this set, it will be possible to compute the skew angle of our document. Given a bounding box of our set, it will also be easy to extract our text from the image and rotate it (probably in a future article).

Preprocessing

Our text is small but we have a large number of points, indeed the resolution of our image is large, we have many pixels per letter. We have several possibilities here: we can downstrongle the image in order to reduce its resolution, we can use mathematical morphology (i.e. erosion), etc. There are certainly other solutions, you will have to choose one depending on what are the previous or next stages in your processing pipeline (e.g. maybe you already have a downstrongled image).

In this article I have chosen to experiment using mathematical morphology for this problem.
We used a 5x3 rectangle shaped structuring element, that is to say we want to keep pixels that lies in a region of white pixels of height 3 and width 5.
Here is the result on the previous image:

Okay, this erosion was really aggressive, we removed most pixels and in fact only some letters "survived" the operation. Calculating the bounding box will be really fast but we may have stripped too much information, it might cause problems on certain images. However as we will see, there are still enough pixels to get decent results.

Implementation

The OpenCV program is similar to the one presented in the previous article.
We declare a compute_skew function that takes as input the path to the image to process, at the beginning of the function we load this image in grayscale, we binarize it and we invert the colors (because objects are represented as white pixels, and the background is represented by black pixels).

void compute_skew(const char* filename)
{
  // Load in grayscale.
  cv::Mat img = cv::imread(filename, 0);
 
  // Binarize
  cv::threshold(img, img, 225, 255, cv::THRESH_BINARY);
 
  // Invert colors
  cv::bitwise_not(img, img);

We can now perform our erosion, we must declare our rectangle-shaped structuring element and call the erode function:

  cv::Mat element = cv::getStructuringElement(cv::MORPH_RECT, cv::Size(5, 3));
  cv::erode(img, img, element);

Now we must create our set of points before calling the function computing the bounding box. As this function cannot be called on an image, we must extract all the positions of our white pixels, this is a great opportunity to present how to scan an image using an iterator:

  std::vector<cv::Point> points;
  cv::Mat_<uchar>::iterator it = img.begin<uchar>();
  cv::Mat_<uchar>::iterator end = img.end<uchar>();
  for (; it != end; ++it)
    if (*it)
      points.push_back(it.pos());

We declare a vector of points in order to store all white pixels. Like when we iterate on a container in C++, we must declare an iterator and also get the iterator representing the end of our container. We use the Mat_ class, note the underscore at the end: it is because it is a templated class: here we must precise the type of the underlying data type. The image has only one channel of size 1 byte, the type is therefore uchar (unsigned char).

We can now use the OpenCV function in order to compute the minimal bounding box, this function is called minAreaRect, this function need a cv::Mat as input so we must convert our vector of points.

  cv::RotatedRect box = cv::minAreaRect(cv::Mat(points));

That's it, we have our minimal bounding box!
We can now have access to the angle:

  double angle = box.angle;
  if (angle < -45.)
    angle += 90.;

During testing I notice I only got negative angle and never below -90 degrees. This is because as we have no reference rectangle, there are several ways to compute the rotation angle. In our case, if the angle is less than -45 degrees, the angle was computed using a "vertical" rectangle, we must therefore correct the angle by adding 90 degrees.

Finally, we will display our bounding rectangle on our eroded image and print the angle on standard output:

  cv::Point2f vertices[4];
  box.points(vertices);
  for(int i = 0; i < 4; ++i)
    cv::line(img, vertices[i], vertices[(i + 1) % 4], cv::Scalar(255, 0, 0), 1, CV_AA);
 
  std::cout << "File " << filename << ": " << angle << std::endl;
  cv::imshow("Result", img);
  cv::waitKey(0);

Note that the line was anti-aliased using CV_AA as the last argument of cv::line.

Results

Using the same 5 images as in the previous article, we obtained the following angles:

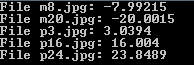
The naming convention for those images is simple, the first letter stands for the sign of the angle (p for plus, m for minus) and the following number is the value of the angle.
The results are not as good as in the previous article, especially with a large angle. Indeed with large values, our preprocessing step (the erosion) will be less meaningful because pixels of a single letter are not vertically or horizontally aligned at all.

Note that the bounding box obtained is not the bounding box of our whole text. The erosion removed a lot of information, if we try to match the bounding box on the initial text, we will lose for example the upper part of letters with a larger height that other letters (e.g. f, t, h, d, l...). Compute the bounding box on the unprocessed text (or use a smaller structuring element) if you want the bounding box of the whole text.