I've recently co-authored an article on the NVIDIA Parallel Forall website: NVIDIA Docker: GPU Server Application Deployment Made Easy.
On the same topic, we presented our work at DockerCon 2016 in the Open Forum track, slides are available here.
I've recently co-authored an article on the NVIDIA Parallel Forall website: NVIDIA Docker: GPU Server Application Deployment Made Easy.
On the same topic, we presented our work at DockerCon 2016 in the Open Forum track, slides are available here.
In this article, I will show how easy it is to cripple or even crash a competing multimedia-oriented application on Android with only a few lines of code.
On Android, in order to do HW decoding, an application must communicate with a process that has access to the HW codecs. However this process is easy to crash if you send it a selected MKV file. It is possible to create an Android service that checks if a competing media player is currently running and then crash the media process, thus stopping HW decoding for this player. As a result, the media player app can also crash and your phone can even reboot.
I have been contributing to the open source projects VLC and VLC for Android in the last few months. I worked on the implementation of an efficient hardware acceleration module for our Android application using the MediaCodec and the OpenMAX APIs. Since your average Android application does not have sufficient permission to access /dev/* entries on your system, you must use a proxy called the mediaserver in order to communicate with HW codecs. The mediaserver works with an IPC mechanism, for instance if you want to perform HW accelerated decoding of an H264 file, you ask the mediaserver to create a decoder and you call methods on this decoder using IPC.
Internally, the mediaserver is using the OpenMAX IL (OMXIL) API to manipulate HW codecs. For HW decoding, userland applications can either use IOMX (OpenMAX over IPC) or the more recent and standardized API called MediaCodec (API level 16).
Using HW accelerated video decoding offers many advantages: you use less battery and you can potentially get significantly better performance. My Nexus 5 phone can only decode 4K videos with HW acceleration. Using the MediaCodec API you can even remove memory copies introduced by the IPC mechanism of mediaserver: you can directly render the frames to an Android surface. Unfortunately, there are also disadvantages: HW codecs are usually less resilient and are more likely to fail if the file is slightly ill-formed. Also, I don't know any HW codec on Android able to handle the Hi10P H264 profile.
The mediaserver on Android also has its own weaknesses: since there is only one process running, if it crashes, all connected clients will suddenly receive an error with almost no chance of recovery. Unfortunately, the mediaserver source code has many calls to CHECK() which is basically assert() but not stripped from release builds. This call is sometimes used to check values that were just read from a file, see for instance the MatroskaExtractor file. When testing HW acceleration for VLC, we noticed random crashes during video playback, sometimes after 20 minutes of flawless HW decoding.
The mediaserver is both easy to crash and essential for all media players applications in order to use HW decoding. Therefore, I realized it would be easy to create a small application that detects if a competing media player is started and then crashes the mediaserver to stop HW decoding. Depending on the app, and on luck too, the media player can crash or decide to fallback to SW. If the video is too large for SW decoding, playback will stutter.
After a bit of testing on the impressive collection of buggy video samples we have at VideoLAN, I found one that deterministically crashes (on my Nexus 5 with 4.4.2, your mileage may vary) the mediaserver when using the MediaScanner API. The sample can be found here. Ironically, it seems to be a test file for the MKV container format:

The evil plan for crashing competing apps can now be achieved with only a few simple steps:
- Starts an Android service (code running in background even if the calling app is not in foreground).
- Frequently monitors which apps are running and looks for known media players like VLC or the Android stock player.
- Uses MediaScannerConnection on the CONT-4G.mkv file, the mediaserver crashes and the media player will immediately receives an error if it was using HW codecs.
I've developed a small test application, and it works fine. Of course, VLC does not use this wicked technique, since it's an open source project you can check yourself in the source code of VLC and VLC for Android.
This looks extreme, and I hope no application will ever use this technique on purpose, but I wanted to show the stability issues we currently encounter with mediaserver. Actually, some services are already regularly crashing the mediaserver on my device, for instance while thumbnailing or extracting metadata from the files on your device; but they don't do that on purpose, I think...
The code is short, first is the main Activity, it simply starts our service:
public class MainActivity extends Activity { @Override public void onCreate(Bundle savedInstanceState) { super.onCreate(savedInstanceState); startService(new Intent(MainActivity.this, MediaCrasherService.class)); Toast toast = Toast.makeText(MainActivity.this, "MediaCrasher service started", Toast.LENGTH_SHORT); toast.show(); finish(); } } |
The service looks at running apps and starts a MediaCrasherConnection with our special file to crash the mediaserver:
public class MediaCrasherService extends IntentService { private class MediaCrasherClient implements MediaScannerConnection.MediaScannerConnectionClient { private String filename; private MediaScannerConnection connection; public MediaCrasherClient(Context ctx, String path) { filename = path; connection = new MediaScannerConnection(ctx, this); connection.connect(); } @Override public void onMediaScannerConnected() { connection.scanFile(filename, null); } @Override public void onScanCompleted(String path, Uri uri) { connection.disconnect(); } } public MediaCrasherService() { super("MediaCrasherService"); } @Override protected void onHandleIntent(Intent intent) { for (int i = 0; i < 12; ++i) { /* Do not run mediacrasher for ever. */ try { Thread.sleep(10000); } catch (InterruptedException e) { /* nothing */ } ActivityManager activityManager = (ActivityManager) this.getSystemService(ACTIVITY_SERVICE); List<RunningAppProcessInfo> procInfos = activityManager.getRunningAppProcesses(); for (int j = 0; j < procInfos.size(); ++j) { RunningAppProcessInfo procInfo = procInfos.get(j); String processName = procInfo.processName; if (procInfo.importance == ActivityManager.RunningAppProcessInfo.IMPORTANCE_FOREGROUND && (processName.equals("org.videolan.vlc") || processName.equals("com.mxtech.videoplayer.ad") || processName.equals("com.inisoft.mediaplayer.a") || processName.equals("com.google.android.videos") || processName.equals("com.google.android.youtube") || processName.equals("com.archos.mediacenter.videofree"))) { String path = "/sdcard/Download/CONT-4G.mkv"; MediaCrasherClient client = new MediaCrasherClient(MediaCrasherService.this, path); } } } } } |
I tested my program on some media players available on Android and here are the results:
- VLC: short freeze and then shows a dialog informing the user that HW acceleration failed and asking him if he wants to restart with SW decoding.
- DicePlayer: freezes the player, force quit is needed.
- MX Player: silent fallback to SW decoding, but the transition is visible since the video goes back in time a few seconds.
- Archos Video Player: reboots your device.
- Play Films: reboots your device.
- Youtube: stops playback, the loading animation never stops and the video display turns black.
I would like to thanks Martin Storsjö and Ludovic Fauvet for their help on Android since I started working on VLC.
In this article we will present a simple code finding an optimal solution to the graph coloring problem using Integer Linear Programming (ILP). We used the GNU Linear Programming Kit (glpk) to solve the ILP problem.
As a project assignment for school we recently had to implement an optimized MPI program given a undirected graph where the edges represent the communications that should take place between MPI processes. For instance this program could be used for a distributed algorithm working on a mesh where each MPI process work on a share of the whole mesh, the edges represent the exchange of boundaries conditions for each iteration.
For a given process, the order of communications with all the neighbours is highly correlated with the performance of the whole program. If all processes start by sending data to the same process, the network bandwidth to this process will be a bottleneck. Therefore it is important to find a good order for communications. Ideally, at each step one process should be involved in only one communication.
By coloring the edges of the graph (all adjacent edges must have different colors), we can find a good scheduling order for MPI communications. Edge coloring can be solved directly, but we have chosen to use the line graph (also called edge-to-vertex dual) instead of the original graph. Therefore we just have to color the vertices of the line graph instead of implementing an edge coloring algorithm.
Initially we implemented a greedy coloring algorithm using the Welsh-Powell heuristic. This algorithm is fast and generally yields fairly good results, but I was interested in getting the optimal solution. Remembering the course I had on linear programming and the research papers I read on register allocation, I decided to use integer linear programming to solve this problem. The proposed implementation is by no means optimized, my goal was to implement a simple but optimal solution using a linear programming library. The final code is approximately 100 lines of code and I think it can be an interesting example for developers that want to start using GLPK.
We need an input format to describe our graph. We used a very simple file format: each line is a vertex, the first number on each line is the identifier of the vertex and the remaining numbers are the neighbours of this vertex. For instance, Wikipedia provides the following example for graph coloring:
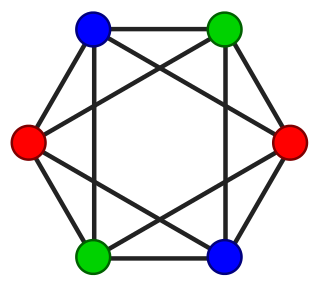
Labelling the vertices from 0 to 5, we obtain the following file:
0 1 2 4 5
1 0 2 3 5
2 0 1 3 4
3 1 2 4 5
4 0 2 3 5
5 0 1 3 4
You will find other graph examples here:
- A bipartite graph (2-colorable, a greedy coloring algorithm can find 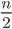 colors).
colors).
- The smallest graph that fails the DSATUR heuristic (3-colorable, DSATUR finds 4 colors).
- The Grötzsch graph (4-colorable).
- Graph 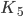 , i.e. complete graph with 5 vertices (5-colorable).
, i.e. complete graph with 5 vertices (5-colorable).
- The Petersen graph (3-colorable).
We implemented the LP formulation given by Mehrotra and Trick (the "VC" formulation).
The number of colors used by our solution is stored in an integer variable 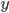 .
.
Given 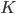 an upper bound on the number of colors needed, we use
an upper bound on the number of colors needed, we use 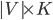 binary variables:
binary variables: 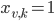 if vertex
if vertex 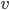 is assigned color
is assigned color 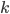 .
.
The objective function is simply:
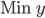
Now we need to define the set of constraints for the graph coloring problem.
With the first constraint we state that each vertex must be assigned exactly one color:
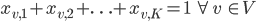
The second constraint is a little tricky, we ensure that we use at most 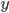 colors by stating that all columns using colors indices greater than
colors by stating that all columns using colors indices greater than 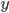 are not used, i.e.:
are not used, i.e.:
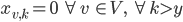
However, we can't use this formula in linear programming so we have to rewrite it:
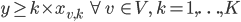
Last but not least, we still need to ensure that adjacent vertices are assigned different colors:
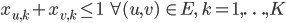
This article is not an introduction to GLPK but the library is simple to use if you have basic knowledge in linear programming, therefore I will not explain the GLPK functions used.
Our function will take as input the graph as a vector of vectors, this the same representation than the input file but with the current vertex index removed from each line.
void color_graph(const std::vector<std::vector<int> >& g) { |
We start by creating a problem object using GLPK and we set up the objective function:
glp_prob* prob = glp_create_prob(); glp_set_obj_dir(prob, GLP_MIN); // minimize |
Before creating variables, we need an upper bound on the number of colors needed for our graph. Every graph can be colored with one more color than the maximum vertex degree, this will be our upper bound:
int num_vertices = g.size(); int max_colors = 0; for (int i = 0; i < num_vertices; ++i) max_colors = std::max(int(g[i].size()) + 1, max_colors); |
As we have an upper bound for integer variable 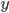 , we can create it and add it to the objective function:
, we can create it and add it to the objective function:
int y = glp_add_cols(prob, 1); glp_set_col_bnds(prob, y, GLP_DB, 1, max_colors); // DB = Double Bound glp_set_obj_coef(prob, y, 1.); glp_set_col_kind(prob, y, GLP_IV); // IV = Integer Variable |
We now need to allocate and set the type of the 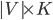 binary variables
binary variables 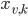 . The indices are stored in a vector of vectors because we will need the indices while creating the constraints:
. The indices are stored in a vector of vectors because we will need the indices while creating the constraints:
std::vector<std::vector<int> > x(num_vertices, std::vector<int>(max_colors)); for (int v = 0; v < num_vertices; ++v) for (int k = 0; k < max_colors; ++k) { x[v][k] = glp_add_cols(prob, 1); glp_set_col_kind(prob, x[v][k], GLP_BV); // BV = Binary Variable } |
To set up the constraints we must build the sparse matrix of coefficients by creating triplets 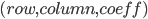 .
.
These triplets are scattered in 3 different vectors. We must insert one element at the beginning because GLPK starts at index 1 after loading the matrix:
std::vector<int> rows(1, 0); std::vector<int> cols(1, 0); std::vector<double> coeffs(1, 0.); |
We now fill the three vectors by adding all the constraints (i.e. the rows) to the matrix, the first constraint:
// One vertex must have exactly one color: // for each vertex v, sum(x(v, k)) == 1 for (int v = 0; v < num_vertices; ++v) { int row_idx = glp_add_rows(prob, 1); glp_set_row_bnds(prob, row_idx, GLP_FX, 1, 1); // FX: FiXed bound for (int k = 0; k < max_colors; ++k) { rows.push_back(row_idx); coeffs.push_back(1); cols.push_back(x[v][k]); } } |
The second constraint:
// We ensure we use y colors max: // for each vertex v and for each color c, // y >= (k + 1) * x(v, k) for (int v = 0; v < num_vertices; ++v) { for (int k = 0; k < max_colors; ++k) { int row_idx = glp_add_rows(prob, 1); glp_set_row_bnds(prob, row_idx, GLP_LO, 0, -1); // LO = LOwer bound rows.push_back(row_idx); coeffs.push_back(1); cols.push_back(y); rows.push_back(row_idx); coeffs.push_back(- k - 1); cols.push_back(x[v][k]); } } |
And now the last set of constraints, this is a bit longer because we iterate on all edges. The graph is undirected but edges are duplicated in our file format, so we must ensure we do not add constraints twice:
// Adjacent vertices cannot have the same color: // for each edge (src, dst) and for each color k, // x(src, k) + x(dst, k) <= 1 for (int src = 0; src < num_vertices; ++src) { const std::vector<int>& succs = g[src]; for (int s = 0; s < succs.size(); ++s) { int dst = succs[s]; // Ensure we don't add both (u, v) and (v, u) if (src > dst) { for (int k = 0; k < max_colors; ++k) { int row_idx = glp_add_rows(prob, 1); glp_set_row_bnds(prob, row_idx, GLP_UP, -1, 1); // UP = UPper bound rows.push_back(row_idx); coeffs.push_back(1); cols.push_back(x[src][k]); rows.push_back(row_idx); coeffs.push_back(1); cols.push_back(x[dst][k]); } } } } |
Everything is now set up! We must now load our sparse matrix into GLPK, ask GLPK to use the floating point solution as the initial solution (presolve) of our ILP problem and start the solver:
glp_load_matrix(prob, rows.size() - 1, &rows[0], &cols[0], &coeffs[0]); glp_iocp parm; glp_init_iocp(&parm); parm.presolve = GLP_ON; glp_intopt(prob, &parm); |
After the last call returns, we have a minimal coloring solution, we can now print the value of 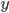 and
and 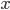 :
:
double solution = glp_mip_obj_val(prob); std::cout << "Colors: " << solution << std::endl; for (int i = 0; i < num_vertices; ++i) { std::cout << i << ": "; for (int j = 0; j < max_colors; ++j) std::cout << glp_mip_col_val(prob, x[i][j]) << " "; std::cout << std::endl; } } |
For instance on the provided bipartite graph we obtain:
Colors: 2
0: 0 1 0 0
1: 0 1 0 0
2: 0 1 0 0
3: 1 0 0 0
4: 1 0 0 0
5: 1 0 0 0
The last two columns are empty, this is because we started with an upper bound 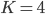 but we used only 2 colors.
but we used only 2 colors.
If you want to run the program, here a small main function to load a graph file and call our coloring algorithm:
int main(int argc, char** argv) { std::vector<std::vector<int> > g; std::ifstream fs(argv[1]); while (true) { std::string line; std::getline(fs, line); if (fs.eof()) break; std::istringstream iss(line); std::istream_iterator<int> begin(iss), eof; g.push_back(std::vector<int>(++begin, eof)); } color_graph(g); } |
To end this article, here are some important points:
- If the initial bounds for 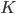 is tight, solving will be faster. For the lower bound you can use 2 instead of 1 if your graph is not edgeless. To find a better upper bound you can use a greedy coloring algorithm before using ILP to find the optimal solution.
is tight, solving will be faster. For the lower bound you can use 2 instead of 1 if your graph is not edgeless. To find a better upper bound you can use a greedy coloring algorithm before using ILP to find the optimal solution.
- If you want to solve the problem faster, use another formulation using column generation.
- If you use C++ you might want to implement your own wrapper above GLPK in order to manipulate variables and constraints easily.
After reading my article, my teacher Anne-Laurence Putz kindly gave me another formulation which is simpler and generally more efficient.
We delete variable 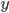 and use the following objective function instead:
and use the following objective function instead:
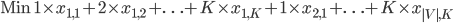
I've written several articles about how to use SSE in C/C++ code, a beginners' tutorial, an explanation on saturation arithmetic with SSE and SSE applied to image processing. In this article I will introduce a new technique to help converting your scalar code to an SSE-accelerated code.
Vectorization is the task of converting a scalar code to a code using SSE instructions. The benefit is that a single instruction will process several elements at the same time (SIMD: Single Instruction, Multiple Data).
Sometimes the compiler manages to transform the scalar code you've written into a vectorized code using SIMD instructions, this process is called auto-vectorization. For example you can read the documentation of GCC to check the status of its tree vectorizer: http://gcc.gnu.org/projects/tree-ssa/vectorization.html, several examples of vectorizable loops are given.
There are a lot of tips to help auto-vectorization: for example rewriting the code to avoid some constructs, using builtins to help the compiler, etc.
But sometimes, despite all your efforts, the compiler cannot vectorize your code. If you really need a performance speedup then you will have to do vectorization by hand using the _mm_* functions. These functions are really low-level so this process can be quite hard and writing an efficient SSE code is difficult.
If you are new to SSE, you might be wondering how conditional code should be vectorized. We will show in this article that this is in fact really easy. You only need to know boolean algebra.
We will attempt to use SSE instructions to speedup the following scalar code:
#include <cmath> void scalar(float* __restrict__ result, const float* __restrict__ v, unsigned length) { for (unsigned i = 0; i < length; ++i) { float val = v[i]; if (val >= 0.f) result[i] = std::sqrt(val); else result[i] = val; } } |
This example is simple: we have a (long) array of floats and we want to compute the square root of each value from these array. Given that a negative number has an imaginary square root, we will only compute the square root of positive values from the array.
Before using SSE instructions, let's see if GCC manages to vectorize our code, we compile the code using the following flags: -O3 -msse3 -ffast-math.
We also use the flag -ftree-vectorizer-verbose=10 to get feedback from the vectorizer on each analyzed loop. Here is the output for our function:
sse.cc:12: note: ===== analyze_loop_nest =====
sse.cc:12: note: === vect_analyze_loop_form ===
sse.cc:12: note: not vectorized: control flow in loop.
sse.cc:12: note: bad loop form.
sse.cc:8: note: vectorized 0 loops in function.
Auto-vectorization failed because of the if statement, we will have to vectorize the code by hand.
Note that if we remove the if (we compute the square root on all elements), then auto-vectorization is successful:
sse.cc:12: note: Cost model analysis:
Vector inside of loop cost: 4
Vector outside of loop cost: 20
Scalar iteration cost: 3
Scalar outside cost: 7
prologue iterations: 2
epilogue iterations: 2
Calculated minimum iters for profitability: 5sse.cc:12: note: Profitability threshold = 4
sse.cc:12: note: Profitability threshold is 4 loop iterations.
sse.cc:12: note: LOOP VECTORIZED.
sse.cc:8: note: vectorized 1 loops in function.
Based on what I've shown in my SSE tutorial, we already know the skeleton of our algorithm: first we need to load 4 float values from memory to a SSE register, then we compute our square root and when we are done we store the result in memory. As a reminder, we will be using the _mm_load_ps function to load from memory to a SSE register and the _mm_store_ps to load from a register to memory (we assume memory accesses are 16-bytes aligned). Our skeleton is therefore as follows:
void sse(float* __restrict__ result, const float* __restrict__ v, unsigned length) { for (unsigned i = 0; i <= length - 4; i += 4) { __m128 vec = _mm_load_ps(v + i); // FIXME: compute square root. _mm_store_ps(result + i, res); } } |
SSE offers a whole range of comparison instructions. These instructions perform 4 comparisons at the same time and the result is stored in another register.
For our vectorization attempt we will use the _mm_cmpge_ps instruction (compare greater or equal):
r0 := (a0 >= b0) ? 0xffffffff : 0x0
r1 := (a1 >= b1) ? 0xffffffff : 0x0
r2 := (a2 >= b2) ? 0xffffffff : 0x0
r3 := (a3 >= b3) ? 0xffffffff : 0x0
If the comparison is true for one pair of values from the operands, all corresponding bits of the result will be set, otherwise the bits are cleared.
The result of the comparison instruction can be used as a logical mask because all the 32 bits corresponding to a float value are set. We can use this mask to conditionally select some floats from a SSE register. In order to vectorize our code, we will use the cmpge instruction and compare 4 values with 0:
__m128 zero = _mm_set1_ps(0.f); __m128 mask = _mm_cmpge_ps(vec, zero); |
(Note: as we are comparing with zero, we could have just used the sign bit here).
The trick is now simple, we perform the square root operation as if there were no negative values:
__m128 sqrt = _mm_sqrt_ps(vec); |
If there were negative values, our sqrt variable is now filled with some NaN values. We simply extract the non-NaN values using a binary AND with our previous mask:
_mm_and_ps(mask, sqrt) |
But, if there were negative values, some values in the resulting register are just 0. We need to copy the values from the original array. We just negate the mask and perform a binary AND with the register containing the original values (variable vec)
_mm_andnot_ps(mask, vec) |
Now we just need to combine the two registers using a binary OR and that's it!
Here is the final code for this function:
void sse(float* __restrict__ result, const float* __restrict__ v, unsigned length) { __m128 zero = _mm_set1_ps(0.f); for (unsigned i = 0; i <= length - 4; i += 4) { __m128 vec = _mm_load_ps(v + i); __m128 mask = _mm_cmpge_ps(vec, zero); __m128 sqrt = _mm_sqrt_ps(vec); __m128 res = _mm_or_ps(_mm_and_ps(mask, sqrt), _mm_andnot_ps(mask, vec)); _mm_store_ps(result + i, res); } } |
Here is a small benchmark to test if our implementation is indeed faster, we tested both implementations on 3 arrays of different size. The CPU used is AMD Phenom II X4 955
| pow(2, 16) | pow(2, 20) | pow(2, 24) | |
| Scalar | 0.428 ms | 6.749 ms | 131.4 ms |
| SSE | 0.116 ms | 2.124 ms | 51.8 ms |
void flush_cache() { static unsigned length = 1 << 26; static char* input = new char[length]; static char* output = new char[length]; memcpy(output, input, length); } |
Thanks to the comparison instructions available with SSE, we can vectorize a scalar code that used a if statement.
Our scalar code was very simple, but if it was at the end of a complicated computation, it would be tempting to perform the square root without SSE on the result vector. We have shown here that this computation can also be done using SSE, thus maximizing parallelism.
In the 3 previous articles I explained how to develop a really simple barcode decoding algorithm. This program was really naive and only worked with really clean barcodes.
As an assignment for a school project, a more advanced version was developed. The program can now detect and decode EAN13 barcodes in large images with various objects and different backgrounds.
Here are the output images of the program. Red rectangles indicates that the segmentation phase detected a potential barcode but the decoding phase rejected it. Green rectangles indicates that a barcode was found and correctly decoded (using the check digit equation, we can detect most decoding errors).
Click on the images for a better view of the output.
As you can see, there were some vicious images :), especially the one with the wooden floor that totally messed up our segmentation, fortunately, the decoding process rejected all those potential barcodes.
The barcodes themselves are sometimes really noisy. If you zoom on some of them you will notice there are large changes in illumination, a low resolution, low contrasts... These problems required an approach much more robust than the one described in the previous articles.
After explaining how the UPC system works in Part 1, I have shown how to decode a digit from an image in Part 2 of this serie. In this article I will now demonstrate how to read the entire barcode.
We will need other helper functions for this last task.
We need a function to skip the quiet zone, skip_value advances the scan pointer to the guard pattern
void skip_quiet_zone(const Mat& img, cv::Point& cur) { while (img(cur) == SPACE) ++cur.x; } |
We need a function to read the left guard and return the smallest width.
unsigned read_lguard(const Mat& img, cv::Point& cur) { int widths[3] = { 0, 0, 0 }; int pattern[3] = { BAR, SPACE, BAR }; for (int i = 0; i < 3; ++i) while (img(cur) == pattern[i]) { ++cur.x; ++widths[i]; } return widths[0]; } |
Here I only return the first width but the best would be to compute the mean. Even better would be to scan the right guard and compute the mean/median of all values. This would be much better for noisy images.
We also need a function to skip the middle guard, note that we don't care about the width right now.
void skip_mguard(const Mat& img, cv::Point& cur) { int pattern[5] = { SPACE, BAR, SPACE, BAR, SPACE }; for (int i = 0; i < 5; ++i) while (img(cur) == pattern[i]) ++cur.x; } |
We have everything we need, the rest is simple: we load the image, we invert it, threshold it, we compute the smallest width with the left guard, we read the 6 left digits, the middle guard, the 6 right digits and that's all ! At the end we print the decoded sequence.
void read_barcode(const std::string& filename) { Mat img = cv::imread(filename, 0); cv::Size size = img.size(); cv::Point cur(0, size.height / 2); cv::bitwise_not(img, img); cv::threshold(img, img, 128, 255, cv::THRESH_BINARY); skip_quiet_zone(img, cur); pattern_map table; setup_map(table); // presented in part 2. int unit_width = read_lguard(img, cur); display(img, cur); std::vector<int> digits; for (int i = 0; i < 6; ++i) { int d = read_digit(img, cur, unit_width, table, LEFT); digits.push_back(d); } skip_mguard(img, cur); for (int i = 0; i < 6; ++i) { int d = read_digit(img, cur, unit_width, table, RIGHT); digits.push_back(d); } for (int i = 0; i < 12; ++i) std::cout << digits[i]; std::cout << std::endl; cv::waitKey(); } |
This reader is simple and far from perfect. There are numerous ways to improve it:
- Use several scan lines. For each bit, compute the median of the intensity found by each scan line.
- We assume we always have a match in our decoding table, we should rather compute the distance to each binary sequence and we should choose the digit with the lowest distance. If we have no digit with a low distance, we can try several digits and see which one satisfies the check digit equation.
- ...
But without doubts, the toughest problem with barcode reading will be concerning preprocessing. The input can be noisy, blurry, skewed, scratched...