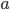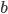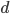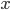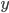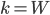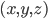In the previous article I explained the basics about the UPC barcode system. In this second part I will show how to read an encoded digit.
UPC Reader
Principle
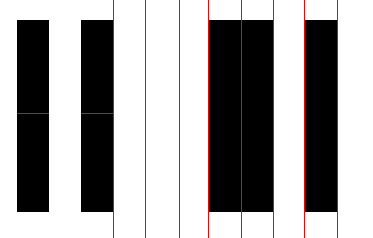
How are going to decode our image ? That's pretty simple, we perform an horizontal scan of our image.
First of all we read the guard in order to find the smallest width and after we read the 6 left digits, the middle guard again and the 6 right digits. To read a digit we read 7 bits and lookup the corresponding digit in a lookup table. Simple !

Digits encoding
First of all we need to store the left and right encoding of each digit, for this purpose we need a std::map (just one because right-encoding is the bitwise complement of left-encoding). The map associates a binary encoding to the value of the digit.
In C++ you can't directly write a binary value (but you can write an hexadecimal value), so I could have just converted the binary sequence in decimal, but for readability I prefer to express the value directly in binary. After a bit of searching I stumbled upon this handy macro:
#define Ob(x) ((unsigned)Ob_(0 ## x ## uL)) #define Ob_(x) (x & 1 | x >> 2 & 2 | x >> 4 & 4 | x >> 6 & 8 | \ x >> 8 & 16 | x >> 10 & 32 | x >> 12 & 64 | x >> 14 & 128) |
To convert the binary sequence 0001101 just write Ob(0001101) !
Here is the code to setup the table:
typedef std::map<unsigned, char> pattern_map; void setup_map(pattern_map& table) { table.insert(std::make_pair(Ob(0001101), 0)); table.insert(std::make_pair(Ob(0011001), 1)); table.insert(std::make_pair(Ob(0010011), 2)); table.insert(std::make_pair(Ob(0111101), 3)); table.insert(std::make_pair(Ob(0100011), 4)); table.insert(std::make_pair(Ob(0110001), 5)); table.insert(std::make_pair(Ob(0101111), 6)); table.insert(std::make_pair(Ob(0111011), 7)); table.insert(std::make_pair(Ob(0110111), 8)); table.insert(std::make_pair(Ob(0001011), 9)); } |
Now we need an...
Helper function
We will need a small helper function in order to assist us while reading a digit.
First of all we will use the following typedef, because we will only be using grayscale/B&W images:
typedef cv::Mat_<uchar> Mat; |
And the two following define (remember we always invert the colors so bars are white !)
#define SPACE 0 #define BAR 255 |
In all following functions, the cur variable is the position of our horizontal scan pointer.
The following function is really helpful in order to prevent error from accumulating after reading a bit.
For example left-digits always end with a '1' bit and we always begin with a '0' bit, therefore if after reading a digit we are still on a bar, we need to advance our scan pointer until we reach the beginning of the next digit. Also, if the previous bit is '0', we have gone too far and we need to decrease our scan pointer in order to be perfectly on the boundary between the two digits.
The situation is reversed for right-digits.
void align_boundary(const Mat& img, cv::Point& cur, int begin, int end) { if (img(cur) == end) { while (img(cur) == end) ++cur.x; } else { while (img(cur.y, cur.x - 1) == begin) --cur.x; } } |
Reading a digit
We now have almost everything we need in order to read a digit, we just need an enum indicating if we are reading a left or a right-encoded digit.
enum position { LEFT, RIGHT }; int read_digit(const Mat& img, cv::Point& cur, int unit_width, pattern_map& table, int position) { // Read the 7 consecutive bits. int pattern[7] = {0, 0, 0, 0, 0, 0, 0}; for (int i = 0; i < 7; ++i) { for (int j = 0; j < unit_width; ++j) { if (img(cur) == 255) ++pattern[i]; ++cur.x; } // See below for explanation. if (pattern[i] == 1 && img(cur) == BAR || pattern[i] == unit_width - 1 && img(cur) == SPACE) --cur.x; } // Convert to binary, consider that a bit is set if the number of // bars encountered is greater than a threshold. int threshold = unit_width / 2; unsigned v = 0; for (int i = 0; i < 7; ++i) v = (v << 1) + (pattern[i] >= threshold); // Lookup digit value. char digit; if (position == LEFT) { digit = table[v]; align_boundary(img, cur, SPACE, BAR); } else { // Bitwise complement (only on the first 7 bits). digit = table[~v & Ob(1111111)]; align_boundary(img, cur, BAR, SPACE); } display(img, cur); return digit; } |
After reading a bit we are using a little trick in order to increase accuracy:
- if we have read only 1 bar and it was the last pixel, we are probably reading the following bit, so move backward by one pixel.
- if we have read only bars except the last pixel, we are probably reading the following bit, so move backward by one pixel.
Warning: I assume here that the smallest width is not 1. This trick should scale with the value of the smallest width.
And now read part 3 for complete decoding !